Треугольник Рело - Reuleaux triangle

Граница треугольника Рело - это кривая постоянной ширины, основанная на равностороннем треугольнике. Все точки на стороне равноудалены от противоположной вершины.

А Треугольник Рело [ʁœlo] это форма, образованная на пересечении трех круговые диски, каждый из которых имеет центр на границе двух других. Его граница - это кривая постоянной ширины, самая простая и известная такая кривая, кроме самого круга.^[1] Постоянная ширина означает, что разделение каждых двух параллельных поддерживающие линии одинаковы, независимо от их ориентации. Поскольку все его диаметры одинаковы, треугольник Рело является одним из ответов на вопрос: «Кроме круга, какая форма может иметь крышка люка сделать так, чтобы он не мог упасть через отверстие? "^[2]

Треугольники Рело также называли сферические треугольники, но этот термин более правильно относится к треугольникам на изогнутой поверхности сфера.Они названы в честь Франц Рёло,^[3] немецкий инженер 19-го века, который был пионером в исследовании машин для преобразования одного типа движения в другой и который использовал в своих конструкциях треугольники Рело.^[4] Однако эти формы были известны и до его времени, например, дизайнерами Готика церковные окна, мимо Леонардо да Винчи, кто использовал его для картографическая проекция, и по Леонард Эйлер в своем исследовании форм постоянной ширины. Другие применения треугольника Рело включают придание формы медиаторы, пожарный гидрант орехи карандаши, и сверла для сверления квадратных отверстий, а также в графическом дизайне в виде некоторых знаков и логотипов компаний.

Среди форм постоянной ширины с заданной шириной треугольник Рело имеет минимальную площадь и самый острый (наименьший) возможный угол (120 °) в углах. По нескольким числовым показателям он дальше всего от центрально-симметричный. Он обеспечивает самую большую форму постоянной ширины, избегая точек целочисленная решетка, и тесно связан с формой четырехугольника, максимизируя отношение периметра к диаметру. Он может совершать полное вращение внутри квадрата, постоянно касаясь всех четырех сторон квадрата, и имеет минимально возможную площадь форм с этим свойством. Однако, хотя он покрывает большую часть квадрата в этом процессе вращения, он не может покрыть небольшую часть площади квадрата около его углов. Из-за этого свойства вращения в квадрате треугольник Рело также иногда называют треугольником. Ротор Reuleaux.^[5]

Треугольник Рело - первый из последовательности Полигоны Reuleaux границы которых представляют собой кривые постоянной ширины, образованные из правильные многоугольники с нечетным количеством сторон. Некоторые из этих кривых использовались в качестве формы монет. Треугольник Рело можно также обобщить в трех измерениях несколькими способами: Тетраэдр Рёло (перекресток четырех мячи чьи центры лежат на регулярном тетраэдр ) не имеет постоянной ширины, но может быть изменен путем скругления его краев для формирования Тетраэдр Мейснера, что делает. В качестве альтернативы поверхность вращения треугольника Рело также имеет постоянную ширину.

Строительство

Чтобы построить треугольник Рело

Треугольник Рело может быть построен либо непосредственно из трех круги, или округлив стороны равносторонний треугольник.^[6]

Построение трех кругов может быть выполнено с помощью компас в одиночку, даже не нуждаясь в линейке. Посредством Теорема Мора – Маскерони то же самое можно сказать и о любом компас и линейка,^[7] но конструкция треугольника Рело особенно проста. Первый шаг - отметить две произвольные точки плоскости (которые в конечном итоге станут вершинами треугольника) и с помощью циркуля начертить круг с центром в одной из отмеченных точек, через другую отмеченную точку. Затем рисуется второй круг того же радиуса с центром в другой отмеченной точке и проходящий через первую отмеченную точку. Наконец, рисуется третий круг, опять же того же радиуса, с центром в одном из двух пересечений. точки двух предыдущих кругов, проходящие через обе отмеченные точки.^[8] Центральная область в получившемся расположении трех окружностей будет треугольником Рело.^[6]

В качестве альтернативы, треугольник Рело может быть построен из равностороннего треугольника. Т нарисовав три дуги окружностей, каждая с центром в одной вершине Т и соединяем две другие вершины.^[9]Или, что то же самое, его можно построить как пересечение трех дисков с центрами в вершинах Т, с радиусом равным длине стороны Т.^[10]

Математические свойства

Параллельный поддерживающие линии треугольника Рело

Самым основным свойством треугольника Рело является то, что он имеет постоянную ширину, что означает, что для каждой пары параллелей поддерживающие линии (две линии с одинаковым наклоном, которые касаются фигуры, но не пересекают ее) две линии имеют одинаковые Евклидово расстояние друг от друга, независимо от ориентации этих линий.^[9] В любой паре параллельных опорных линий одна из двух линий обязательно будет касаться треугольника в одной из его вершин. Другая опорная линия может касаться треугольника в любой точке противоположной дуги, и их расстояние (ширина треугольника Рело) равно радиусу этой дуги.^[11]

Первый математик, открывший существование кривых постоянной ширины и обнаруживший, что треугольник Рело имеет постоянную ширину, возможно, был Леонард Эйлер.^[5] В статье, которую он представил в 1771 году и опубликовал в 1781 году под названием De Curvis triangularibus, Эйлер изучал криволинейный треугольники, а также кривые постоянной ширины, которые он назвал круговыми.^[12][13]

Экстремальные меры

По многим параметрам треугольник Рело - одна из самых крайних кривых постоянной ширины.

Посредством Теорема Бляшке – Лебега, треугольник Рело имеет наименьшую возможную площадь любой кривой заданной постоянной ширины. Эта область

${\displaystyle {\frac {1}{2}}(\pi -{\sqrt {3}})s^{2}\approx 0.70477s^{2},}$

куда s постоянная ширина. Один из методов вывода этой формулы площади состоит в том, чтобы разделить треугольник Рело на внутренний равносторонний треугольник и три криволинейные области между этим внутренним треугольником и дугами, образующими треугольник Рело, а затем сложить площади этих четырех наборов. С другой стороны, кривая постоянной ширины с максимально возможной площадью представляет собой круглый диск, который имеет площадь ${\displaystyle \pi s^{2}/4\approx 0.78540s^{2}}$.^[14]

Углы, образованные каждой парой дуг в углах треугольника Рело, равны 120 °. Это самый острый угол при любом вершина любой кривой постоянной ширины.^[9] Кроме того, среди кривых постоянной ширины треугольник Рело имеет как самый большой, так и самый маленький вписанные равносторонние треугольники.^[15] Самый большой равносторонний треугольник, вписанный в треугольник Рело, - это тот, который соединяет его три угла, а самый маленький - тот, который соединяет эти три угла. средние точки его сторон. Подмножество треугольника Рело, состоящее из точек, принадлежащих трем или более диаметрам, является внутренней частью большего из этих двух треугольников; она имеет большую площадь, чем набор точек трех диаметров любой другой кривой постоянной ширины.^[16]

Центрально-симметричные формы внутри и снаружи треугольника Рело, используемые для измерения его асимметрии.

Хотя треугольник Рело шестикратен двугранная симметрия, так же, как равносторонний треугольник, у него нет центральная симметрия Треугольник Рело - это наименее симметричная кривая постоянной ширины в соответствии с двумя различными мерами центральной асимметрии: Мера Ковнера – Безиковича (отношение площади к наибольшему центрально-симметричный форма, заключенная в кривую) и Мера Эстермана (отношение площади к наименьшей центрально-симметричной форме, охватывающей кривую). Для треугольника Рело две центрально-симметричные формы, определяющие меры асимметрии, являются шестиугольник, хотя внутренняя имеет загнутые стороны.^[17] Треугольник Рело имеет диаметры, которые делят его площадь более неравномерно, чем любая другая кривая постоянной ширины. То есть максимальное соотношение площадей по обе стороны от диаметра, еще одна мера асимметрии, для треугольника Рело больше, чем для других кривых постоянной ширины.^[18]

Среди всех форм постоянной ширины, избегающих всех точек целочисленная решетка, наибольшая ширина - это треугольник Рело. Он имеет одну из осей симметрии, параллельную осям координат на полуцелой прямой. Его ширина, приблизительно 1,545, является корнем полинома шестой степени с целыми коэффициентами.^[17][19][20]

Точно так же, как круг может быть окружен шестью совпадающими кругами, которые касаются его, можно также расположить семь конгруэнтных треугольников Рело так, чтобы все они соприкасались с центральным треугольником Рело того же размера. Это максимально возможное число для любой кривой постоянной ширины.^[21]

An равнодиагональный летающий змей который максимизирует отношение периметра к диаметру, вписанный в треугольник Рело

Среди всего четырехугольники, форма, имеющая наибольшее соотношение периметр к его диаметр является равнодиагональный летающий змей которое можно вписать в треугольник Рело.^[22]

Прочие меры

От Теорема Барбье все кривые одинаковой постоянной ширины, включая треугольник Рело, имеют равную периметры. В частности, этот периметр равен периметру круга той же ширины, которая равна ${\displaystyle \pi s}$.^[23][24][9]

Радиусы наибольшего вписанный круг треугольника Рело шириной s, и из описанный круг того же треугольника, являются

${\displaystyle \displaystyle \left(1-{\frac {1}{\sqrt {3}}}\right)s\approx 0.42265s\quad {\text{and}}\quad \displaystyle {\frac {s}{\sqrt {3}}}\approx 0.57735s}$

соответственно; сумма этих радиусов равна ширине треугольника Рело. В более общем смысле, для каждой кривой постоянной ширины наибольший вписанный круг и наименьший описанный круг являются концентрическими, а их радиусы суммируются с постоянной шириной кривой.^[25]

Нерешенная проблема в математике: Насколько плотно треугольники Рело могут быть упакованы в плоскости? (больше нерешенных задач по математике)

Оптимальный плотность упаковки треугольника Рело на плоскости остается недоказанным, но предполагается, что он

${\displaystyle {\frac {2(\pi -{\sqrt {3}})}{{\sqrt {15}}+{\sqrt {7}}-{\sqrt {12}}}}\approx 0.922888,}$

что является плотностью одного из возможных двойная решетка упаковка для этих форм. Лучшая проверенная верхняя граница плотности упаковки составляет приблизительно 0,947275.^[26] Было также высказано предположение, но не доказано, что треугольники Рело имеют самую высокую плотность упаковки из всех кривых постоянной ширины.^[27]

Вращение внутри квадрата

Вращение треугольника Рело внутри квадрата с отображением кривой, очерченной центром треугольника

Любая кривая постоянной ширины может образовывать ротор внутри квадрат, фигура, которая может совершать полный поворот, оставаясь внутри квадрата и всегда касаясь всех четырех сторон квадрата. Однако треугольник Рело - это ротор с минимально возможной площадью.^[9] Во время вращения его ось не остается неподвижной в одной точке, а вместо этого следует кривой, образованной частями четырех эллипсы.^[28] Из-за углов в 120 ° вращающийся треугольник Рело не может достичь некоторых точек рядом с более острыми углами в вершинах квадрата, а скорее покрывает форму со слегка закругленными углами, также образованную эллиптическими дугами.^[9]

Один из четырех эллипсов, за которым следует центр вращающегося треугольника Рело в квадрате.

Эллипс, отделяющий один из углов (нижний левый) квадрата от области, охватываемой вращающимся треугольником Рело

В любой момент во время этого поворота два угла треугольника Рело касаются двух соседних сторон квадрата, а третий угол треугольника очерчивает кривую около противоположной вершины квадрата. Форма, очерченная вращающимся треугольником Рело, покрывает примерно 98,77% площади квадрата.^[29]

Как контрпример

Первоначальная мотивация Рело к изучению треугольника Рело была в качестве контрпримера, показывающего, что трех одноточечных контактов может быть недостаточно, чтобы зафиксировать плоский объект в одном положении.^[30] Существование треугольников Рело и других кривых постоянной ширины показывает, что измерения диаметра сами по себе не могут подтвердить, что объект имеет круглое поперечное сечение.^[31]

В связи с вписанная квадратная задача, Эгглстон (1958) заметил, что треугольник Рело представляет собой пример формы постоянной ширины, в которую нельзя вписать правильный многоугольник с более чем четырьмя сторонами, кроме правильного шестиугольника, и описал небольшую модификацию этой формы, которая сохраняет ее постоянную ширину, но также предотвращает правильные шестиугольники от вписания в него. Он обобщил этот результат на три измерения, используя цилиндр той же формы, что и его поперечное сечение.^[32]

Приложения

Достигая углов

Некоторые типы машин имеют форму треугольника Рело, основанного на его способности вращаться внутри квадрата.

В Watts Brothers Tool Works квадрат сверло имеет форму треугольника Рело, измененного с вогнутостями для образования режущих поверхностей. При установке в специальный патрон, который позволяет долоту не иметь фиксированного центра вращения, она может просверлить отверстие почти квадратной формы.^[33] Хотя он был запатентован Генри Уоттсом в 1914 году, подобные сверла, изобретенные другими, использовались и раньше.^[9] Другие многоугольники Reuleaux используются для сверления пятиугольных, шестиугольных и восьмиугольных отверстий.^[9][33]

Panasonic РУЛО робот-пылесос имеет форму, основанную на треугольнике Рело, чтобы облегчить уборку пыли в углах комнаты.^[34][35]

Цилиндры качения

Сравнение цилиндрического ролика и ролика с треугольником Рело

Другой класс приложений треугольника Рело - это цилиндрические объекты с поперечным сечением треугольника Рело. Несколько карандашей производятся именно этой формы, а не более традиционных круглых или шестиугольных стержней.^[36] Их обычно продвигают как более удобные или способствующие правильному захвату, а также как меньшую вероятность скатывания со стола (поскольку центр тяжести перемещается вверх и вниз больше, чем катящийся шестиугольник).

Треугольник Рело (вместе со всеми остальными кривые постоянной ширины ) может рулон но делает колесо плохим, потому что оно не катится вокруг фиксированного центра вращения. Объект на роликах, имеющих поперечное сечение треугольника Рело, будет катиться плавно и ровно, но ось, прикрепленная к колесам треугольника Рело, будет подпрыгивать вверх и вниз три раза за оборот.^[9][37] Эта концепция была использована в научно-фантастическом рассказе Пол Андерсон под названием «Трёхугольное колесо».^[11][38] Велосипед с плавающими осями и рамой, поддерживаемой ободом колеса в форме треугольника Рело, был построен и продемонстрирован в 2009 году китайским изобретателем Гуан Байхуа, которого вдохновили карандаши той же формы.^[39]

Конструкция механизма

Механизм продвижения пленки на основе треугольника Рило в 8-мм кинопроекторе Советский Луч-2

Другой класс приложений треугольника Рело включает его использование как часть механическая связь что может преобразовать вращение вокруг фиксированной оси в возвратно-поступательное движение.^[10] Эти механизмы изучал Франц Рёло. При содействии компании Gustav Voigt, Reuleaux построил около 800 моделей механизмов, некоторые из которых были связаны с треугольником Reuleaux.^[40] Рило использовал эти модели в своих новаторских научных исследованиях их движения.^[41] Хотя большая часть моделей Рело – Фойгта утеряна, 219 из них были собраны на Корнелл Университет, в том числе девять на основе треугольника Рило.^[40][42] Однако использование треугольников Рело в конструкции механизмов предшествовало работе Рело; например, некоторые Паровые двигатели с 1830 г. кулачок в форме треугольника Рело.^[43][44]

Одно из применений этого принципа возникает в кинопроектор. В этом приложении необходимо продвигать пленку рывками, пошагово, при этом каждый кадр пленки останавливается на долю секунды перед объективом проектора, а затем гораздо быстрее пленка перемещается к следующему. Рамка. Это можно сделать с помощью механизма, в котором вращение треугольника Рело внутри квадрата используется для создания модели движения для исполнительного механизма, который быстро подтягивает пленку к каждому новому кадру, а затем приостанавливает движение пленки во время проецирования кадра.^[45]

Ротор Двигатель Ванкеля имеет форму криволинейного треугольника, который часто приводят в качестве примера треугольника Рело.^{[3][5][9][44]} Однако его изогнутые стороны несколько более плоские, чем у треугольника Рело, и поэтому он не имеет постоянной ширины.^[46]

Архитектура

Окно в форме треугольника Рело Церковь Богоматери, Брюгге в Бельгии

В Готическая архитектура, начиная с конца 13 или начала 14 века,^[47] Треугольник Рело стал одной из нескольких криволинейных форм, часто используемых для окон, оконных узор, и другие архитектурные украшения.^[3] Например, в Английская готическая архитектура эта форма была связана с декорированным периодом, как в геометрическом стиле 1250–1290 годов, так и продолжающемся в его криволинейном стиле 1290–1350 годов.^[47] Он также появляется в некоторых окнах Миланский собор.^[48] В этом контексте форму чаще называют сферическим треугольником,^[47][49][50] но более обычное математическое значение сферический треугольник треугольник на поверхности сфера (форма также обычно используется в архитектуре как удерживающий ). При использовании в готической церковной архитектуре, треугольная форма треугольника Рело может рассматриваться как символ Троица,^[51] и как «акт противостояния форме круга».^[52]

Треугольник Рело также использовался в других стилях архитектуры. Например, Леонардо да Винчи набросал эту форму как план укрепления.^[42] Современные здания, которые, как утверждается, используют план этажа в форме треугольника Рело, включают MIT Kresge Auditorium, то Kölntriangle, то Donauturm, то Торре-де-Коллсерола, а Музей Mercedes-Benz.^[53] Однако во многих случаях это просто закругленные треугольники с другой геометрией, чем треугольник Рело.

Картографирование

Основная статья: октантная проекция

Еще одно раннее применение треугольника Рело, карта мира да Винчи примерно с 1514 г. карта мира в котором сферическая поверхность земли была разделена на восемь октантов, каждый из которых был сплющен в форме треугольника Рело.^[54][55][56]

Леонардо карта мира да Винчи в восьми квадрантах треугольника Рело

Подобные карты, также основанные на треугольнике Рело, были опубликованы Оронс Фине в 1551 г. и к Джон Ди в 1580 г.^[56]

Другие объекты

Треугольник Рело медиаторы

Много медиаторы используйте треугольник Рело, так как его форма сочетает в себе острый острие, обеспечивающее сильную артикуляцию, с широким острием для получения теплого тембра. Поскольку все три точки формы можно использовать, ее легче ориентировать, и она изнашивается менее быстро по сравнению с киркой с одним наконечником.^[57]

Незаконное использование пожарного гидранта, Филадельфия, 1996 г., и более нового гидранта из Филадельфии с гайкой в ​​форме треугольника Рело для предотвращения такого использования.

Треугольник Рело использовался как форма поперечного сечения пожарный гидрант гайка клапана. Постоянная ширина этой формы затрудняет открытие пожарного гидранта с помощью стандартных гаечных ключей с параллельными губками; вместо этого нужен гаечный ключ особой формы. Это свойство позволяет открывать пожарные гидранты пожарным (у которых есть специальный гаечный ключ), но не другим людям, пытающимся использовать гидрант в качестве источника воды для других целей.^[58]

В Субмиллиметровая матрица, с семью из восьми антенн, расположенными приблизительно на треугольнике Рело.

По предложению Кето (1997),^[59] усики Субмиллиметровая матрица, радиоволновая астрономическая обсерватория на Мауна-Кеа в Гавайи, расположены на четырех вложенных треугольниках Рело.^[60][61] Размещение антенн на кривой постоянной ширины позволяет обсерватории иметь одинаковое пространственное разрешение во всех направлениях и обеспечивает круговой луч наблюдения. Как наиболее асимметричная кривая постоянной ширины, треугольник Рело приводит к наиболее равномерному покрытию плоскости для преобразование Фурье сигнала от массива.^[59][61] Антенны можно перемещать из одного треугольника Рело в другой для различных наблюдений в соответствии с желаемым угловым разрешением каждого наблюдения.^[60][61] Точное размещение антенн на этих треугольниках Рело было оптимизировано с помощью нейронная сеть. В некоторых местах построенная обсерватория отклоняется от предпочтительной формы треугольника Рело, потому что такая форма была невозможна на данном участке.^[61]

Знаки и логотипы

Форма щита, используемая для многих знаков и корпоративных логотипов, представляет собой закругленные треугольники. Однако лишь некоторые из них являются треугольниками Рело.

Корпоративный логотип Петрофина (Fina), бельгийская нефтяная компания с основными операциями в Европе, Северной Америке и Африке, использовала треугольник Рело с названием Fina с 1950 года до слияния Petrofina с Total S.A. в 2000 г.^[62][63]Еще один корпоративный логотип, обрамленный треугольником Рило, направленным на юг. компас из Бавария пивоварня, был частью модернизации дизайнерской компании Total Identity, получившей награду SAN 2010 Advertiser of the Year.^[64] Треугольник Рело также используется в логотипе Колорадская горная школа.^[65]

В Соединенных Штатах Национальная система трасс и Система велосипедных маршрутов США оба обозначают маршруты треугольниками Рило на указателях.^[66]

В природе

Треугольник Рело как центральный пузырь в математической модели плоского кластера мыльных пузырей из четырех пузырьков

Согласно с Законы Плато, дуги окружности в двумерном мыльный пузырь кластеры встречаются под углами 120 °, таким же углом находится в углах треугольника Рело. Исходя из этого факта, можно построить кластеры, в которых часть пузырьков принимает форму треугольника Рело.^[67]

Форма была впервые выделена в форме кристалла в 2014 году в виде дисков треугольника Рело.^[68] Базовый нитрат висмута диски в форме треугольника Рело были сформированы из гидролиз и атмосферные осадки нитрата висмута в системе этанол – вода в присутствии 2,3-бис (2-пиридил) пиразина.

Обобщения

Треугольные кривые постоянной ширины с гладкими, а не острыми углами могут быть получены как геометрическое место точек на фиксированном расстоянии от треугольника Рело.^[69] Другие обобщения треугольника Рело включают поверхности в трех измерениях, кривые постоянной ширины с более чем тремя сторонами и множества Янмути, которые предоставляют крайние примеры неравенства между шириной, диаметром и внутренним радиусом.

Трехмерная версия

Четыре шара пересекаются, образуя тетраэдр Рело.

Перекресток четырех мячи радиуса s с центром в вершинах регулярного тетраэдр с длиной стороны s называется Тетраэдр Рёло, но его поверхность не поверхность постоянной ширины.^[70] Однако его можно превратить в поверхность постоянной ширины, называемую Тетраэдр Мейснера, путем замены трех его краевых дуг на изогнутые поверхности, поверхности вращения дуги окружности. В качестве альтернативы поверхность вращения треугольник Рело, проходящий через одну из его осей симметрии, образует поверхность постоянной ширины с минимальным объемом среди всех известных поверхностей вращения данной постоянной ширины.^[71]

Полигоны Reuleaux

Основная статья: Многоугольник Рило

Полигоны Reuleaux

Объединенные Арабские Эмираты 50 филс Reuleaux семиугольник монета

Треугольник Рило можно обобщить на правильные или неправильные многоугольники с нечетным числом сторон, что дает Многоугольник Рило, кривая постоянной ширины, образованная дугами окружности постоянного радиуса. Постоянная ширина этих форм позволяет использовать их в качестве монет в монетоприемниках.^[9] Хотя монеты этого типа в общем обращении обычно имеют более трех сторон, треугольник Рело использовался для памятных монет из Бермуды.^[53]

Аналогичные методы можно использовать для включения произвольного простой многоугольник внутри кривой постоянной ширины, ширина которой равна диаметру данного многоугольника. Результирующая форма состоит из дуг окружности (не более чем сторон многоугольника), может быть построена алгоритмически в линейное время, и может быть нарисован с помощью циркуля и линейки.^[72] Хотя все многоугольники Рело имеют нечетное количество сторон дуги окружности, можно построить фигуры постоянной ширины с четным количеством сторон дуги окружности различных радиусов.^[73]

Yanmouti наборы

Множества Янмути определяются как выпуклые оболочки равностороннего треугольника вместе с тремя дугами окружности, центрированными в вершинах треугольника и охватывающими тот же угол, что и треугольник, с равными радиусами, которые не более чем равны длине стороны треугольника. Таким образом, когда радиус достаточно мал, эти множества вырождаются в сам равносторонний треугольник, но когда радиус настолько велик, насколько это возможно, они равны соответствующему треугольнику Рело. Каждая форма с шириной ш, диаметр d, а по радиусу р (радиус наибольшего возможного круга, содержащегося в форме) подчиняется неравенству

${\displaystyle w-r\leq {\frac {d}{\sqrt {3}}},}$

и это неравенство становится равенством для множеств Янмоути, показывая, что его нельзя улучшить.^[74]

Связанные цифры

Triquetra переплетены, чтобы сформировать трилистник

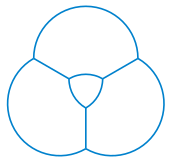
В классическом представлении трех комплектов Диаграмма Венна в виде трех перекрывающихся кругов центральная область (представляющая элементы, принадлежащие всем трем множествам) принимает форму треугольника Рело.^[3] Те же три круга образуют один из стандартных рисунков Кольца Борромео, три взаимосвязанных кольца, которые, однако, не могут быть реализованы в виде геометрических окружностей.^[75] Части этих же кругов используются для формирования Triquetra, фигура трех перекрывающихся полукруги (каждые два из которых образуют vesica piscis символ), в центре которого снова находится треугольник Рело;^[76] Точно так же, как три окружности диаграммы Венна могут быть переплетены, чтобы образовать кольца Борромео, три дуги окружностей трикетры могут быть переплетены, чтобы сформировать трилистник.^[77]

Родственники треугольника Рело возникают в проблеме поиска минимальной формы периметра, которая охватывает фиксированную площадь и включает три заданные точки на плоскости. Для широкого диапазона выбора параметра площади оптимальным решением этой проблемы будет изогнутый треугольник, три стороны которого представляют собой дуги окружности с одинаковыми радиусами. В частности, когда три точки равноудалены друг от друга, а площадь равна площади треугольника Рело, треугольник Рело является оптимальным ограждением.^[78]

Круглые треугольники представляют собой треугольники с ребрами в виде дуги окружности, включая треугольник Рело, а также другие формы. дельтовидная дуга это другой тип криволинейного треугольника, но тот, в котором кривые, заменяющие каждую сторону равностороннего треугольника, вогнутые, а не выпуклые. Он не состоит из дуг окружности, но может быть образован путем катания одного круга внутри другого, радиус которого в три раза превышает радиус.^[79] Другие плоские формы с тремя изогнутыми сторонами включают арбелос, который формируется из трех полукруги с коллинеарными конечными точками,^[80] и Треугольник Безье.^[81]

Треугольник Рело можно также интерпретировать как конформный образ из сферический треугольник с углами 120 °.^[67] Этот сферический треугольник - один из Треугольники Шварца (с параметрами 3/2, 3/2, 3/2), треугольники, ограниченные дугами большого круга на поверхности сферы, которые могут покрывать сферу путем отражения.^[82]

Рекомендации

1. Гарднер (2014) называет это самым простым, а Грубер (1983, п. 59) называет это «самым громким».
2. Клее, Виктор (1971), «Формы будущего», Двухлетний математический журнал колледжа, 2 (2): 14–27, Дои:10.2307/3026963, JSTOR  3026963.
3. Альсина, Клауди; Нельсен, Роджер Б. (2011), Иконы математики: исследование двадцати ключевых образов, Математические экспозиции Дольчиани, 45, Математическая ассоциация Америки, п. 155, ISBN  978-0-88385-352-8.
4. Луна, Ф. К. (2007), Машины Леонардо да Винчи и Франца Рёло: кинематика машин от эпохи Возрождения до 20 века, История механизма и машиноведения, 2, Спрингер, ISBN  978-1-4020-5598-0.
5. Брайант, Джон; Сангвин, Крис (2011), Насколько круглый ваш круг? Где встречаются инженерия и математика, Издательство Принстонского университета, п. 190, ISBN  978-0-691-14992-9.
6. Хэнн, Майкл (2014), Структура и форма в дизайне: важнейшие идеи для творческой практики, A&C Black, стр. 34, ISBN  978-1-4725-8431-1.
7. Hungerbühler, Norbert (1994), "Краткое элементарное доказательство теоремы Мора-Машерони", Американский математический ежемесячный журнал, 101 (8): 784–787, CiteSeerX  10.1.1.45.9902, Дои:10.2307/2974536, JSTOR  2974536, МИСТЕР  1299166.
8. Эта конструкция кратко описывается Маор и Йост (2014) и это можно увидеть, например, на видео Развлечение с треугольниками Рило Автор Alex Franke, 21 августа 2011 г.
9. Гарднер, Мартин (2014), «Глава 18: Кривые постоянной ширины», Узлы и кольца Борромео, реплики и восемь королев, Новая математическая библиотека Мартина Гарднера, 4, Cambridge University Press, стр. 223–245, ISBN  978-0-521-75613-6.
10. Клее, Виктор; Вагон, С. (1991), Старые и новые нерешенные задачи плоской геометрии и теории чисел, Математические экспозиции Дольчиани, 11, Cambridge University Press, стр. 21, ISBN  978-0-88385-315-3.
11. Маор, Эли; Йост, Ойген (2014), «Треугольник Рило, 46», Красивая геометрия, Princeton University Press, стр. 154–156, ISBN  978-1-4008-4833-1.
12. Райх, Карин (2007), «Вклад Эйлера в дифференциальную геометрию и его восприятие», в Bradley, Robert E .; Сандифер, Эд (ред.), Леонард Эйлер: жизнь, работа и наследие, Исследования по истории и философии математики, 5, Elsevier, стр. 479–502, Дои:10.1016 / S0928-2017 (07) 80026-0, ISBN  9780444527288. См., В частности, раздел 1.4, «Орбиформы, 1781 год», стр. 484–485.
13. Эйлер, Леонард (1781), "De Curvis triangularibus", Acta Academiae Scientiarum Imperialis Petropolitanae (на латыни), 1778: 3–30. См., В частности, стр. 7 для определения орбиформ.
14. Грубер, Питер М. (1983), Выпуклость и ее приложения, Биркхойзер, стр.67, ISBN  978-3-7643-1384-5
15. Грубер (1983, п. 76)
16. Макеев, В. В. (2000), "Экстремальное свойство треугольника Рело", Зап. Научн. Сем. С.-Петербург. Отдел. Мат. Inst. Стеклова. (ПОМИ), 267 (Геом. И Топол. 5): 152–155, 329, Дои:10.1023 / А: 1021287302603, МИСТЕР  1809823, S2CID  116027099.
17. Финч, Стивен Р. (2003), «8.10 Константы треугольника Рело» (PDF), Математические константы, Энциклопедия математики и ее приложений, Cambridge University Press, стр.513–514, ISBN  978-0-521-81805-6.
18. Groemer, H .; Валлен, Л. Дж. (2001), "Мера асимметрии для областей постоянной ширины", Beiträge zur Algebra und Geometrie, 42 (2): 517–521, МИСТЕР  1865537.
19. Грубер (1983, п. 78)
20. Салли, Г. Т. (1969), «Максимальный набор постоянной ширины в решетке», Тихоокеанский математический журнал, 28 (3): 669–674, Дои:10.2140 / pjm.1969.28.669, МИСТЕР  0240724.
21. Фейес Тот, Л. (1967), «О количестве одинаковых дисков, которые могут коснуться другого такого же типа», Studia Scientiarum Mathematicarum Hungarica, 2: 363–367, МИСТЕР  0221388; Шопп, Дж. (1970), "Über die Newtonsche Zahl einer Scheibe konstanter Breite", Studia Scientiarum Mathematicarum Hungarica (на немецком), 5: 475–478, МИСТЕР  0285983.
22. Болл, Д. (1973), «Обобщение π», Математический вестник, 57 (402): 298–303, Дои:10.2307/3616052, JSTOR  3616052; Гриффитс, Дэвид; Калпин, Дэвид (1975), "Pi-оптимальные многоугольники", Математический вестник, 59 (409): 165–175, Дои:10.2307/3617699, JSTOR  3617699.
23. Лэй, Стивен Р. (2007), Выпуклые множества и их приложения, Довер, теорема 11.11, стр. 81–82, ISBN  978-0-486-45803-8.
24. Барбье, Э. (1860 г.), "Note sur le problème de l'aiguille et le jeu du Joint Couvert" (PDF), Journal de Mathématiques Pures et Appliquées, 2^е série (на французском языке), 5: 273–286. См., В частности, стр. 283–285.
25. Lay (2007), Теорема 11.8, стр. 80–81.
26. Слепой, G .; Слепой, Р. (1983), "Eine Abschätzung für die Dichte der dichtesten Packung mit Reuleaux-Dreiecken", Studia Scientiarum Mathematicarum Hungarica (на немецком), 18 (2–4): 465–469, МИСТЕР  0787951. Смотрите также Слепой, G .; Слепой, Р. (1987), "Reguläre Packungen mit Reuleaux-Dreiecken", Результаты по математике (на немецком), 11 (1–2): 1–7, Дои:10.1007 / BF03323256, МИСТЕР  0880190, S2CID  121633860.
27. Резникофф, Говард Л. (2015), О кривых и поверхностях постоянной ширины, arXiv:1504.06733, Bibcode:2015arXiv150406733R.
28. Гляйфтнер, Винфрид; Цайтлер, Герберт (май 2000 г.), «Треугольник Рело и его центр масс», Результаты по математике, 37 (3–4): 335–344, Дои:10.1007 / bf03322004, S2CID  119600507.
29. Пиковер, Клиффорд А. (2009), «Треугольник Рело», Книга по математике: от Пифагора до 57-го измерения, 250 вех в истории математики, Sterling Publishing Company, стр. 266, ISBN  978-1-4027-5796-9.
30. Луна (2007), п. 239.
31. Грановский, В. А .; Siraya, T. N., "Метрологическая прослеживаемость и качество измерений промышленных испытаний", в Pavese, F .; Bär, M .; Filtz, J.-R .; Forbes, A.B .; Pendrill, L .; Широно, К. (ред.), Передовые математические и вычислительные инструменты в метрологии и тестировании IX, World Scientific, стр. 194–201.. См. В частности п. 200.
32. Эгглстон, Х. Г. (1958), «Фигуры, вписанные в выпуклые множества», Американский математический ежемесячный журнал, 65 (2): 76–80, Дои:10.2307/2308878, JSTOR  2308878, МИСТЕР  0097768.
33. Как просверлить отверстия в квадратном шестиугольнике, восьмиугольнике, пятиугольнике, Уилмердинг, Пенсильвания: Watts Brothers Tool Works, 1950–1951 (Брошюра на 27 страницах).
34. Мотидзуки, Такаши (22 января 2015 г.), «Panasonic выпускает треугольный робот-пылесос», Япония в реальном времени, Wall Street Journal.
35. Коксворт, Бен (3 марта 2015 г.), «Panasonic вступает в игру роботов-пылесосов с треугольным руло», Гизмаг.
36. Гамбер, Джонни (26 апреля 2006 г.), «Отзыв о Staedtler Noris Ergosoft HB», Карандашная революция, получено 2015-05-22.
37. Масферрер Леон, Клаудиа; фон Вутенау Майер, Себастьян (декабрь 2005 г.), «Новое изобретение колеса: некруглые колеса», Математический интеллект, 27 (4): 7–13, Дои:10.1007 / bf02985852.
38. Андерсон, Пол (октябрь 1963 г.), "Трехугольное колесо", Аналоговый, стр. 50–69
39. Демпстер, Тайра (17 июня 2009 г.), Китаец изобретает велосипед заново, Reuters
40. Луна, Фрэнсис К. (июль 1999 г.), Коллекция кинематических механизмов Рило в Корнельском университете (PDF), Библиотека Корнельского университета, архив из оригинал (PDF) 14 июня 2020 г..
41. Хендерсон, Дэвид В .; Таймина, Дайна (2007), «Ощущение смыслов в геометрии», в Синклер, Натали; Пимм, Дэвид; Хиггинсон, Уильям (ред.), Математика и эстетика: новые подходы к древнему родству, CMS Книги по математике, Springer, стр. 58–83, Дои:10.1007/978-0-387-38145-9_4, HDL:1813/2714, ISBN  978-0-387-38145-9. См. В частности п. 81 год.
42. Луна (2007, п. 241).
43. Луна (2007, п. 240)
44. Петерсон, Иварс (19 октября 1996 г.), "Катание с Рило", MathTrek, НаукаНовости. Перепечатано в Петерсон, Иварс (2002), Математические пути: от сюрреалистических чисел к волшебным кругам, Спектр МАА, Математическая ассоциация Америки, стр. 141–144, ISBN  978-0-88385-537-9.
45. Lay (2007), п. 83.
46. Грубер (1983, п. 80); Нэш, Дэвид Х. (март 1977 г.), "Геометрия роторного двигателя", Математический журнал, 50 (2): 87–89, Дои:10.1080 / 0025570x.1977.11976621; Бадр, О ​​.; Naik, S .; O'Callaghan, P.W .; Проберт, С. Д. (1991), "Роторные двигатели Ванкеля как расширительные устройства в паровых двигателях цикла Ренкина", Прикладная энергия, 39 (1): 59–76, Дои:10.1016/0306-2619(91)90063-4.
47. Харт, Стивен (2010), Средневековая церковная ажурная церковь в Англии, Boydell & Brewer Ltd, стр. 63–64, ISBN  978-1-84383-533-2.
48. Маркетти, Елена; Коста, Луиза Росси (2014), «Какая геометрия в Миланском соборе?», Уильямс, Ким; Оствальд, Майкл Дж. (ред.), Архитектура и математика от античности до будущего, том I: от древности до 1500-х годов, Birkhäuser, стр. 509–534, Дои:10.1007/978-3-319-00137-1_35
49. Паркер, Джон Генри (1850), Словарь терминов, используемых в греческой, римской, итальянской и готической архитектуре., 1 (5-е изд.), Лондон: Дэвид Роуг, стр. 202.
50. Берчетт, Э. С. (1876 г.), Практическая геометрия плоскости, Лондон и Глазго: Уильям Коллинз, сыновья и компания, подпись к пластине LV, рис..
51. Дюран, Гийом (1906), Символика церквей и церковных украшений: перевод первой книги Rationale Divinorum Officiorum (3-е изд.), Гиббингс, стр. lxxxviii.
52. Франкл, Пол; Кроссли, Пол (2000), Готическая архитектура, Пеликан история искусства, 19, Издательство Йельского университета, стр. 146, ISBN  978-0-300-08799-4.
53. Конти, Джузеппе; Паолетти, Раффаэлла (октябрь 2019 г.), «Треугольник Рило в архитектуре и приложениях», Магнаги-Дельфино, Паола; Мел, Джампьеро; Норандо, Туллия (ред.), Грани геометрии: от Аньези до Мирзахани, Конспект лекций по сетям и системам, Springer, стр. 79–89, Дои:10.1007/978-3-030-29796-1_7
54. Снайдер, Джон П. (1997), Сглаживание Земли: две тысячи лет картографических проекций, University of Chicago Press, стр. 40, ISBN  978-0-226-76747-5.
55. Кёнинг, Йоханнес (январь 1955 г.), "История географических картографических проекций до 1600 г.", Имаго Мунди, 12 (1): 1–24, Дои:10.1080/03085695508592085, JSTOR  1150090.
56. Бауэр, Дэвид И. (февраль 2012 г.), «Необычная проекция для одной из карт Джона Ди 1580 года» (PDF), Картографический журнал, 49 (1): 55–61, Дои:10.1179 / 1743277411y.0000000015, S2CID  129873912.
57. Гувер, Уилл (ноябрь 1995 г.), Picks !: Красочная сага о старинных гитарных плекторах из целлулоида, Backbeat Books, стр. 32–33, ISBN  978-0-87930-377-8.
58. Мартини, Хорст; Монтехано, Луис; Оливерос, Дебора (2019), Тела постоянной ширины: введение в выпуклую геометрию с приложениями, Биркхойзер, стр. 3, Дои:10.1007/978-3-030-03868-7, ISBN  978-3-030-03866-3, МИСТЕР  3930585
59. Кето, Эрик (1997), "Формы взаимно корреляционных интерферометров", Астрофизический журнал, 475 (2): 843–852, Bibcode:1997ApJ ... 475..843K, Дои:10.1086/303545.
60. Бланделл, Раймонд (2007), «Субмиллиметровая матрица» (PDF), Proc. 2007 IEEE / MTT-S Международный симпозиум по микроволновому излучению, стр. 1857–1860, Дои:10.1109 / mwsym.2007.380132, ISBN  978-1-4244-0687-6, S2CID  41312640.
61. Ho, Paul T. P .; Моран, Джеймс М .; Ло, Квок Юнг (2004), «Субмиллиметровая антенная решетка», Астрофизический журнал, 616 (1): L1 – L6, arXiv:Astro-ph / 0406352, Bibcode:2004ApJ ... 616L ... 1H, Дои:10.1086/423245, S2CID  115133614.
62. Гвиллиан, Сэм (16 мая 2015 г.), Интересный материал: кривые постоянной ширины, Радио Ньюпорта, архивировано с оригинал 16 июня 2016 г.
63. "История логотипа Fina: от Petrofina до Fina", Итого: групповая презентация, Total S.A., архивировано с оригинал 26 декабря 2012 г., получено 31 октября 2015.
64. «В мире: Бавария, фундаментальный ребрендинг в Баварии», Полная идентичность, заархивировано из оригинала 30.06.2015, получено 2015-06-27
65. Фишер, Роланд Б. (весна 2002 г.), «M-blems: Объяснение логотипа» (PDF), Шахты: Журнал Горной школы Колорадо, т. 92 нет. 2, стр. 29, архивировано 10 июля 2010 г.
66. Линдли, Джеффри А. (1 июня 2012 г.), «Информация: MUTCD - Промежуточное разрешение на использование альтернативной конструкции для знака« Велосипедный маршрут (M1-9) в США »(IA-15)», Руководство по унифицированным устройствам управления движением на улицах и автомагистралях: ресурсы, Министерство транспорта США, Федеральное управление шоссейных дорог, получено 20 августа, 2018
67. Modes, Carl D .; Камиен, Рэндалл Д. (2013), «Сферические пены в плоском пространстве», Мягкая материя, 9 (46): 11078–11084, arXiv:0810.5724, Bibcode:2013SMat .... 911078M, Дои:10.1039 / c3sm51585k, S2CID  96591302.
68. Ng, C.H.B .; Фан, W. Y. (2014), "Диски треугольника Рело: новая форма на блоке", Журнал Американского химического общества, 136 (37): 12840–12843, Дои:10.1021 / ja506625y, PMID  25072943.
69. Банчофф, Томас; Гиблин, Питер (1994), "О геометрии кусочно-круговых кривых", Американский математический ежемесячный журнал, 101 (5): 403–416, Дои:10.2307/2974900, JSTOR  2974900, МИСТЕР  1272938.
70. Вебер, Кристоф (2009), Какое отношение имеет это твердое тело к мячу? (PDF) Вебер также пленки обоих типов вращающихся тел Мейснера а также интерактивные изображения.
71. Кампи, Стефано; Колесанти, Андреа; Гронки, Паоло (1996), "Минимальные задачи для объемов выпуклых тел", Уравнения в частных производных и приложения: Сборник статей в честь Карло Пуччи, Конспект лекций по чистой и прикладной математике, вып. 177, Марсель Деккер, стр. 43–55..
72. Chandru, V .; Венкатараман, Р. (1991), «Круглые корпуса и орбиты простых многоугольников», Материалы второго ежегодного симпозиума ACM-SIAM по дискретным алгоритмам (SODA '91), Филадельфия, Пенсильвания, США: Общество промышленной и прикладной математики, стр. 433–440, ISBN  978-0-89791-376-8.
73. Петерсон, Брюс Б. (1973), «Свойства пересечения кривых постоянной ширины», Иллинойсский журнал математики, 17 (3): 411–420, Дои:10.1215 / ijm / 1256051608, МИСТЕР  0320885.
74. Эрнандес Сифре, М.А. (2000), «Существует ли плоский выпуклый набор с заданной шириной, диаметром и внутренним радиусом?», Американский математический ежемесячный журнал, 107 (10): 893–900, Дои:10.2307/2695582, JSTOR  2695582, МИСТЕР  1806918.
75. Линдстрем, Бернт; Зеттерстрём, Ханс-Олов (1991), «Круги Борромео невозможны», Американский математический ежемесячный журнал, 98 (4): 340–341, Дои:10.2307/2323803, JSTOR  2323803.
76. Вайсштейн, Эрик В., «Трикетра», MathWorld
77. Хой, Джессика; Миллет, Кеннет С. (2014), «Математический анализ узлов и связывания в картеле Леонардо да Винчи Академии Винчиана» (PDF), Журнал математики и искусств.
78. Курант, Ричард; Роббинс, Герберт (1996), Что такое математика? Элементарный подход к идеям и методам (2-е изд.), Oxford University Press, стр. 378–379, ISBN  978-0-19-975487-8.
79. Локвуд, Э. Х. (1961), "Глава 8: Дельтовидная мышца", Книга кривых, Издательство Кембриджского университета
80. Маккей, Дж. С. (февраль 1884 г.), «Нож сапожника», Труды Эдинбургского математического общества, 3: 2, Дои:10,1017 / с0013091500037196.
81. Брюйнс, Дж. (1998), "Квадратичные треугольники Безье как примитивы рисования", Материалы семинара ACM SIGGRAPH / EUROGRAPHICS по графическому оборудованию (HWWS '98), Нью-Йорк, Нью-Йорк, США: ACM, стр. 15–24, Дои:10.1145/285305.285307, ISBN  978-1-58113-097-3, S2CID  28967106.
82. Веннингер, Магнус Дж. (2014), Сферические модели, Дувр, стр. 134, ISBN  978-0-486-14365-1.

внешняя ссылка

• Вайсштейн, Эрик В., "Треугольник Рело", MathWorld