Логистическая дистрибуция - Logistic distribution

Логистика

Функция плотности вероятности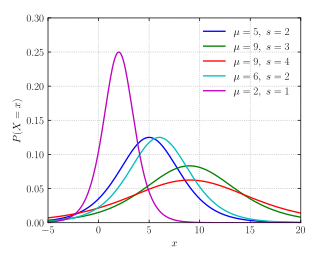
Кумулятивная функция распределения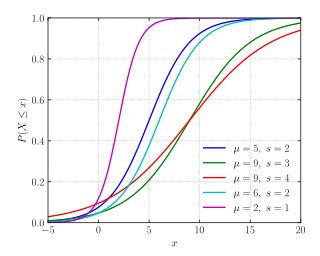
Параметры	${\displaystyle \mu ,}$ место расположения (настоящий ) ${\displaystyle s>0,}$ шкала (настоящий)
Поддерживать	${\displaystyle x\in (-\infty ,\infty )}$
PDF	${\displaystyle {\frac {e^{-(x-\mu )/s}}{s\left(1+e^{-(x-\mu )/s}\right)^{2}}}}$
CDF	${\displaystyle {\frac {1}{1+e^{-(x-\mu )/s}}}}$
Иметь в виду	${\displaystyle \mu }$
Медиана	${\displaystyle \mu }$
Режим	${\displaystyle \mu }$
Дисперсия	${\displaystyle {\frac {s^{2}\pi ^{2}}{3}}}$
Асимметрия	${\displaystyle 0}$
Бывший. эксцесс	${\displaystyle 6/5}$
Энтропия	${\displaystyle \ln s+2}$
MGF	${\displaystyle e^{\mu t}\mathrm {B} (1-st,1+st)}$ за ${\displaystyle t\in (-1/s,1/s)}$ и ${\displaystyle \mathrm {B} }$ это Бета-функция
CF	${\displaystyle e^{it\mu }{\frac {\pi st}{\sinh(\pi st)}}}$

В теория вероятности и статистика, то логистическая дистрибуция - непрерывное распределение вероятностей. Его кумулятивная функция распределения это логистическая функция, который появляется в логистическая регрессия и нейронные сети с прямой связью. Он напоминает нормальное распределение по форме, но имеет более тяжелые хвосты (выше эксцесс ). Логистическая дистрибуция - это частный случай Лямбда-распределение Тьюки.

Технические характеристики

Функция плотности вероятности

Когда параметр местоположенияμ равен 0, а параметр масштабаs равно 1, то функция плотности вероятности логистического распределения определяется

${\displaystyle {\begin{aligned}f(x;0,1)&={\frac {e^{-x}}{(1+e^{-x})^{2}}}\\[4pt]&={\frac {1}{(e^{x/2}+e^{-x/2})^{2}}}\\[5pt]&={\frac {1}{4}}\operatorname {sech} ^{2}\left({\frac {x}{2}}\right).\end{aligned}}}$

Таким образом, в целом плотность составляет:

${\displaystyle {\begin{aligned}f(x;\mu ,s)&={\frac {e^{-(x-\mu )/s}}{s\left(1+e^{-(x-\mu )/s}\right)^{2}}}\\[4pt]&={\frac {1}{s\left(e^{(x-\mu )/(2s)}+e^{-(x-\mu )/(2s)}\right)^{2}}}\\[4pt]&={\frac {1}{4s}}\operatorname {sech} ^{2}\left({\frac {x-\mu }{2s}}\right).\end{aligned}}}$

Поскольку эту функцию можно выразить через квадрат гиперболическая секущая функция «сечь», иногда его называют сеч-квадрат (d) распределение.^[1]

Смотрите также: гиперболическое секущее распределение

Кумулятивная функция распределения

Логистическая дистрибуция получила свое название от кумулятивная функция распределения, который является экземпляром семейства логистических функций. Кумулятивная функция распределения логистического распределения также является масштабированной версией гиперболический тангенс.

${\displaystyle F(x;\mu ,s)={\frac {1}{1+e^{-(x-\mu )/s}}}={\frac {1}{2}}+{\frac {1}{2}}\operatorname {tanh} \left({\frac {x-\mu }{2s}}\right).}$

В этом уравнении Икс это случайная переменная, μ - иметь в виду, и s - масштабный параметр, пропорциональный стандартное отклонение.

Квантильная функция

В обратный кумулятивная функция распределения (квантильная функция ) логистического распределения является обобщением логит функция. Его производная называется функцией плотности квантиля. Они определены следующим образом:

${\displaystyle Q(p;\mu ,s)=\mu +s\ln \left({\frac {p}{1-p}}\right).}$

${\displaystyle Q'(p;s)={\frac {s}{p(1-p)}}.}$

Альтернативная параметризация

Альтернативная параметризация логистического распределения может быть получена путем выражения параметра масштаба, ${\displaystyle s}$, в единицах стандартного отклонения, ${\displaystyle \sigma }$, используя замену ${\displaystyle s\,=\,q\,\sigma }$, куда ${\displaystyle q\,=\,{\sqrt {3}}/{\pi }\,=\,0.551328895\ldots }$. Альтернативные формы вышеупомянутых функций достаточно просты.

Приложения

Логистическое распределение - и S-образный узор его кумулятивная функция распределения (в логистическая функция ) и квантильная функция (в функция logit ) - широко использовались во многих различных областях.

Логистическая регрессия

Одно из самых распространенных приложений - в логистическая регрессия, который используется для моделирования категоричный зависимые переменные (например, варианты ответа "да-нет" или выбор из 3 или 4 вариантов), почти как стандартный линейная регрессия используется для моделирования непрерывные переменные (например, доход или население). В частности, модели логистической регрессии можно сформулировать как скрытая переменная модели с переменные ошибки после логистического распределения. Эта формулировка распространена в теории дискретный выбор модели, в которых логистическое распределение играет ту же роль в логистической регрессии, что и нормальное распределение делает в пробит регрессия. Действительно, логистическое и нормальное распределения имеют очень похожую форму. Однако логистическая дистрибуция более тяжелые хвосты, что часто увеличивает надежность основанных на нем анализов по сравнению с использованием нормального распределения.

Физика

PDF этого распределения имеет ту же функциональную форму, что и производная от Функция Ферми. В теории свойств электронов в полупроводниках и металлах эта производная устанавливает относительный вес различных энергий электронов в их вкладах в перенос электронов. Те уровни энергии, энергии которых наиболее близки к «среднему» распределения (Уровень Ферми ) доминируют над такими процессами, как электронная проводимость, с некоторым размытием, вызванным температурой.^[2]:34 Обратите внимание, однако, что соответствующие вероятность распространение в Статистика Ферми – Дирака на самом деле простой Распределение Бернулли, с коэффициентом вероятности, заданным функцией Ферми.

Логистическое распределение возникает как предельное распределение случайного движения с затуханием конечной скорости, описываемого телеграфным процессом, в котором случайные моменты времени между последовательными изменениями скорости имеют независимые экспоненциальные распределения с линейно увеличивающимися параметрами.^[3]

Гидрология

Подогнанное кумулятивное логистическое распределение для осадков в октябре с использованием CumFreq, смотрите также Распределительная арматура

В гидрология распределение долгосрочного речного стока и осадков (например, месячные и годовые итоговые значения, состоящие из суммы 30 или 360 дневных значений) часто считается почти нормальным в соответствии с Центральная предельная теорема.^[4] В нормальное распределение Однако требуется числовое приближение. Поскольку логистическое распределение, которое можно решить аналитически, похоже на нормальное распределение, его можно использовать вместо него. На синем рисунке показан пример подгонки логистического распределения к ранжированным дождевым осадкам в октябре, которые распределяются почти нормально, и он показывает 90% пояс уверенности на основе биномиальное распределение. Данные об осадках представлены построение позиций как часть совокупный частотный анализ.

Шахматные рейтинги

В Федерация шахмат США а ФИДЕ изменила формулу расчета шахматных рейтингов с нормального распределения на логистическое распределение; см. статью о Система рейтинга Эло (сам основан на нормальном распределении).

Связанные дистрибутивы

• Логистическое распределение имитирует sech распространение.
• Если Икс ~ Логистика (μ, β) тогда kX + ℓ ~ Логистика (kμ + ℓ, kβ).
• Если Икс ~ U(0, 1) тогда μ + β(бревно(Икс) - журнал (1 - Икс)) ~ Логистика (μ, β).
• Если ${\displaystyle X\sim \mathrm {Gumbel} (\alpha _{X},\beta )}$ и ${\displaystyle Y\sim \mathrm {Gumbel} (\alpha _{Y},\beta )}$ тогда ${\displaystyle X-Y\sim \mathrm {Logistic} (\alpha _{X}-\alpha _{Y},\beta )\,}$.
• Если ${\displaystyle X}$ и ${\displaystyle Y\sim \mathrm {Gumbel} (\alpha ,\beta )}$ тогда ${\displaystyle X+Y\nsim \mathrm {Logistic} (2\alpha ,\beta )\,}$ (Сумма нет логистическое распределение). Обратите внимание, что ${\displaystyle E(X+Y)=2\alpha +2\beta \gamma \neq 2\alpha =E\left(\mathrm {Logistic} (2\alpha ,\beta )\right)}$.
• Если Икс ~ Логистика (μ, s), затем exp (Икс) ~ LogLogistic${\displaystyle \left(\alpha =e^{\mu },\beta ={\frac {1}{s}}\right)}$, и exp (Икс) + γ ~ смещенная логистика

${\displaystyle \left(\alpha =e^{\mu },\beta ={\frac {1}{s}},\gamma \right)}$.

• Если Икс ~ Экспоненциальный (1) тогда

${\displaystyle \mu +\beta \log(e^{X}-1)\sim \operatorname {Logistic} (\mu ,\beta ).}$

• Если Икс, Y ~ Экспоненциальная (1), тогда

${\displaystyle \mu -\beta \log \left({\frac {X}{Y}}\right)\sim \operatorname {Logistic} (\mu ,\beta ).}$

Производные

Моменты высшего порядка

В пЦентральный момент -й порядок может быть выражен через функцию квантили:

${\displaystyle {\begin{aligned}\operatorname {E} [(X-\mu )^{n}]&=\int _{-\infty }^{\infty }(x-\mu )^{n}\,dF(x)\\&=\int _{0}^{1}{\big (}Q(p)-\mu {\big )}^{n}\,dp=s^{n}\int _{0}^{1}\left[\ln \!\left({\frac {p}{1-p}}\right)\right]^{n}\,dp.\end{aligned}}}$

Этот интеграл хорошо известен^[5] и может быть выражено через Числа Бернулли:

${\displaystyle \operatorname {E} [(X-\mu )^{n}]=s^{n}\pi ^{n}(2^{n}-2)\cdot |B_{n}|.}$

Смотрите также

• Обобщенная логистическая дистрибуция
• Лямбда-распределение Тьюки
• Логистическая регрессия
• Логистическая дистрибуция
• Сигмовидная функция

Примечания

1. Джонсон, Котц и Балакришнан (1995, стр.116).
2. Дэвис, Джон Х. (1998). Физика низкоразмерных полупроводников: введение. Издательство Кембриджского университета. ISBN  9780521484916.
3. А. Ди Крещенцо, Б. Мартинуччи (2010) "Затухающий телеграфный случайный процесс с логистическим стационарным распределением", J. Appl. Вероятность., т. 47. С. 84–96.
4. Ритзема, Х.П., изд. (1994). Частотный и регрессионный анализ. Глава 6 в: Принципы и применение дренажа, Публикация 16, Международный институт мелиорации и улучшения земель (ILRI), Вагенинген, Нидерланды. стр.175–224. ISBN  90-70754-33-9.
5. OEIS: A001896

Рекомендации

• Джон С. ДеКани и Роберт А. Стайн (1986). «Заметка о выводе информационной матрицы для логистической дистрибуции». Американский статистик. Американская статистическая ассоциация. 40: 220–222. Дои:10.2307/2684541.
• Н., Балакришнан (1992). Справочник по логистике. Марсель Деккер, Нью-Йорк. ISBN  0-8247-8587-8.
• Johnson, N.L .; Kotz, S .; Н., Балакришнан (1995). Непрерывные одномерные распределения. Vol. 2 (2-е изд.). ISBN  0-471-58494-0.

• Модис, Теодор (1992) Прогнозы: контрольная подпись общества раскрывает прошлое и предсказывает будущее, Саймон и Шустер, Нью-Йорк. ISBN  0-671-75917-5